Un título un poco críptico para este post. No es en absoluto casualidad, como podréis comprobar en los próximos días. El título se refiere a las posibilidades que tengo de acertar los 6 números de la primitiva, que son del 50%: o me toca o no me toca. A raíz de un comentario de Juanjo, hace ya algún tiempo que prometí hablar de esta falacia (gran chiste para los matemáticos) y me la he encontrado esta mañana en la portada del Sport.
Aunque no han sido tan brutos como para decir que las probabilidades de que el Barcelona gane la liga son del 50% (o la gana o la pierde), han incurrido en la misma falacia. Veamos: El error al decir que me puede tocar la primitiva o no al 50% está en suponer que los dos casos son equiprobables, cuando en realidad solo hay una forma de que me toque (salen mis 6 números), pero hay algo así como 13.983.815 formas de que no me toque (sale cualquier otra combinación).
Simplifiquemos para verlo más claro: Si decimos que la probabilidad de que al tirar un dado salga un 1 es del 50%, estamos olvidando que solo hay una forma de acertar (sale un 1), pero hay 5 formas de no acertar (sale 2, 3, 4, 5 o 6), por lo que los sucesos “salir 1” y “no salir 1” no son equiprobables.
Volvemos al Sport. Según ellos, las probabilidades de que gane el Barcelona son del 33%, las del Real Madrid del 59% y las del Sevilla, del 7% (no os preocupe que entre los tres sólo sumen el 99%: no hay ningún otro equipo que pueda ganarla, es solo que se han comido los decimales). ¿De dónde obtienen estos resultados? Fácil: haciendo una tabla con “todos” los casos posibles, a saberse: que gane el Madrid, gane el Barcelona y gane el Sevilla; que ganen el Madrid y el Barcelona y empate el Sevilla, etc… Imagino que habéis pillado la idea. Se obtiene la siguiente tabla, cortesía del diario As (que, por cierto, cae en el mismo error, pero se cuida mucho de no hablar de probabilidades, así que es correcto):
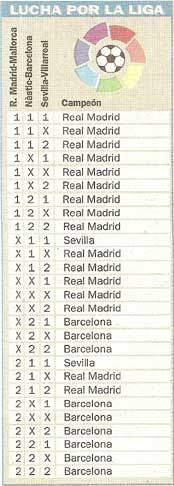Hay 27 casos posibles, de los cuales el Real Madrid ganaría en 16, el Barcelona en 9 y el Sevilla en 2. De ahí las posibilidades de las que habla el Sport. Ahora bien, eso sería correcto en el caso de que esas 27 opciones fueran equiprobables, de modo que la pregunta es: ¿Es igual de probable el caso 1-2-1 (ganan los tres candidatos) que el X-X-X (empatan los tres)?
Y no lo digo porque suponga que el Madrid, el Barcelona o el Sevilla son mejores que sus rivales y sea más probable que ganen a que empaten, me limito a las matemáticas.El fútbol consiste en meter una esfera (o balón) por un hueco rectangular (portería). Para ello contamos con 11 personas. Este hecho sería fácil (para ellos) y aburrido (para los espectadores) si no fuese por que tenemos a otras 11 personas que tratan de impedirlo (el otro equipo). Esas otras 11 personas son las que convierten un sencillo problema de geometría en una difícil hazaña: Meter un gol no es fácil (o no debe serlo, según deducimos por su escasez, pocas veces se pasa de 10 en hora y media). Entonces, ¿es igual de probable un empate que un 1 o un 2?
Analicemos el número de goles:
– Si en el partido no hay goles, los sucesos 1-X-2 no son igual de probables, de hecho es casi seguro que acabe en empate.
– Si en el partido hay 1 gol, el resultado puede ser 1-0 o 0-1, es decir, un 1 o un 2, pero es imposible una X.
– Con 2 goles, tenemos como posibilidades 2-0 (un 1), 1-1 (una X) o 0-2 (un 2). En este caso sí son igual de probables.
– Con 3 goles, puede ocurrir 3-0 (1), 2-1 (1), 1-2 (2) o 0-3 (2). De nuevo no hay posibilidad de empate.
– Con 4 goles, tenemos 4-0 y 3-1 para un 1, 2-2 para una X y 1-3 y 0-4 para un 2.
Si continuamos, vemos que el empate solo puede ocurrir cuando el número de goles es par y, en esos casos, es menos probable que el 1 o el 2, porque solo se puede empatar de una forma, pero se puede ganar (o perder) de varias.
Por lo tanto, la combinación X-X-X no es igual de probable que la 1-1-1, por ejemplo. Repito que esto es sólo matemáticamente, sin tener en cuenta que unos equipos sean mejores que otros y que, en consecuencia, sea más probable que ganen a que pierdan. Si tenemos en cuenta eso, el análisis matemático de probabilidades se hace imposible. De modo que, aunque hoy “puede ocurrir cualquier cosa”, no es fácil hablar de porcentajes ni de probabilidades numéricas. Que gane el mejor, o el menos malo.
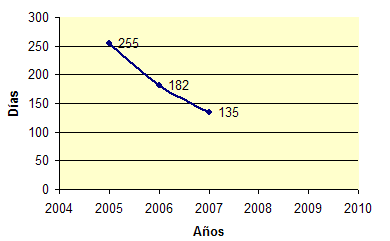
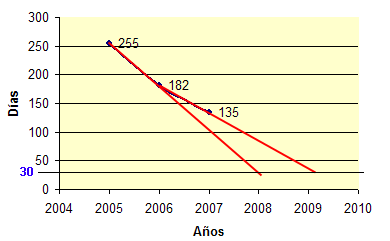
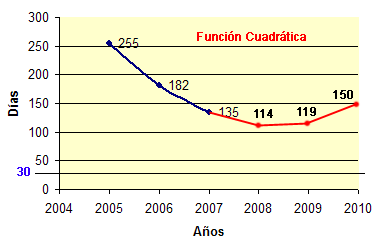
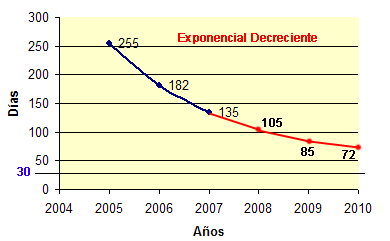
PD: por si alguién quiere conocer mi opinión, os diré que no me gusta el fútbol, pero este año me he interesado por los resultados porque, cuando quedaban 14 partidos, haciendo un análisis matemático de la situación (que incluía factores psicológicos), un par de rectas y unas gráficas, y asumiendo un error de Tipo I, dije (aseguré) que iba a ganar la liga el Real Madrid. Podéis imaginar las risas y las burlas en aquel entonces (sin problema, porque solo se lo decía a gente conocida). Con el tiempo, pasaron a decir “puede ser” y hoy me decían que “puede ser que no”. Ellos saben perfectamente que ni me gusta ni entiendo de fútbol, y siempre les he dicho que mi pronostico era matemático, no futbolístico. Quedan unas horas para conocer al ganador y para que unas cuantas personas de mi entorno (espero) se tomen las matemáticas un poco más en serio.
Loading...
RSS: Entradas