Hace unos días pude ver la película danesa “En un mundo mejor” (Hævnen), dirigida por Susanne Bier. Hace tiempo que quería verla porque ganó el Oscar y el Globo de Oro a la Mejor Película de habla no inglesa, y la verdad es que no decepciona. Si tenéis oportunidad de verla, no os la perdáis. Yo me voy a quedar ahora con una escena que podemos ver al principio del film, en la que el profesor presenta al nuevo alumno a sus compañeros:
¡Qué casualidad! ¡Su cumpleaños es el mismo día que el de otro compañero! Parece muy poco probable, entre 365 días del año, que coincidan los cumpleaños de dos personas el mismo día, pero la verdad es que es más probable que ocurra a que no ocurra, si el grupo tiene más de 23 personas. Si el grupo es de 25 personas, la probabilidad de que haya dos personas que cumplan años el mismo día es del 57%. Si el grupo es de 30 personas, esa probabilidad sube al 71%, y si tenemos 35 personas, al 81’5%. Es decir, en un grupo de 35 personas, la probabilidad de que dos de ellas cumplan años el mismo día es del 81’5%, mientras que la probabilidad de que todos tengan cumpleaños diferentes sólo es del 18’5%.
¿Cómo es posible? Pues es una cuestión de probabilidades: La primera persona, puede nacer cualquier día, nunca va a coincidir con nadie. Tiene entonces, 365 opciones de 365. La segunda, en cambio, ya solo tiene 364 posibilidades si no quiere coincidir con el primero. El tercero tendrá 363 de los 365 días del año para elegir. El cuarto solo 362 y así sucesivamente. La persona número 30, como ya habrá 29 fechas ocupadas, tendrá libres 336 días de los 365 para no coincidir con ningunos de los demás. Si calculamos esta probabilidad, la de que todos cumplan años en fechas distintas, tenemos que es el producto de las 30 fracciones:
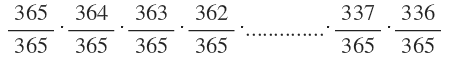
que da, aproximadamente, 0’29. Por lo tanto, si las probabilidades de que no coincidan cumpleaños son del 29%, la probabilidad de que coincida alguno es del 71%, que no es tan pequeña para que nos sorprenda tanto.
Ya véis, las probabilidades tienen estas cosas, pero como no saberlas no es problema en la sociedad, si alguien se sorprende por algo que es normal, nadie se da cuenta. Si alguien dijera, por ejemplo, “¡Anda! Romeo y Julieta también lo escribió Shakespeare, el mismo de Hamlet. ¡Qué casualidad!”, ¿pasaría lo mismo?
Por eso seguimos creyendo en la suerte, las casualidades y demás explicaciones a hechos “sorprendentes” que las matemáticas ya explican bastante bien.






 RSS: Entradas
RSS: Entradas
Pingback: probabilidad | mate3isabel's Blog