Herramienta para calcular el término general de una progresión aritmética conociendo algunos datos de la misma. Rellena las casillas correspondientes a los datos que conozcas y pulsa “Calcular”:
Explicación:
Se llaman progresiones aritméticas a aquellas sucesiones de números en las que cada término se va obteniendo sumando una cantidad fija al anterior. Por ejemplo,
6, 8, 10, 12, 14, 16… (vamos sumando 2)
15, 12, 9, 6, 3, 0, -3… (vamos sumando -3)
A esa cantidad fija que sumamos se le llama diferencia y se le asigna la letra “d”. Así, en el primer ejemplo tenemos que d=2 y en el segundo d=-3.
El término que ocupa un lugar cualquiera n de la sucesión se llama an. Así, el término que ocupa el lugar 8 es el a8 y el término vigésimo es a20. El primer término es, por supuesto, a1.
Como a2=a1+d, a3=a1+d+d, a4=a1+d+d+d, etc, es fácil hallar el término general de una progresión aritmética si conocemos dónde comienza (a1) y cuánto sumamos cada vez (d), ya que partiendo de a1, para llegar al término n tenemos que sumar (n-1) veces la cantidad d. Es decir, tenemos que:
an = a1 + (n – 1) · d
En el caso de que no nos den a1 y d, pero nos dan, por ejemplo, a8 y d, sustituyendo en la fórmula anterior podemos despejar a1. Si no nos dieran ni a1 ni d, sino que nos dan dos términos cualesquiera, por ejemplo, a6 y a15, sustituyendo en la fórmula anterior podemos plantear un sistema de dos ecuaciones con dos incógnitas (a1 y d) y calcularlas.
Suma de n términos de una progresión aritmética:
Si nos fijamos, en una progresión aritmética cualquiera, por ejemplo:
4, 7, 10, 13, 16, 19, 22, 25, 28, 31…
la suma del primer término con el último es la misma que la del segundo con el penúltimo, e igual a la del tercero con el antepenúltimo, etc. En este ejemplo, (4 + 31) = (7 + 28) = (10 + 25) = … = 35, pero puedes comprobar que esto se cumple con todas las progresiones aritméticas, pongas los términos que pongas.
De este modo, si queremos sumar los anteriores números:
4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31
emparejandolos como hemos visto tenemos:
(4 + 31) + (7 + 28) + (10 + 25) + (13 + 22) + (16 + 19)
es decir:
35 + 35 + 35 + 35 + 35
No es difícil comprobar que tenemos que multiplicar 35 por el número de parejas que hemos hecho. En este caso, como queríamos sumar 10 términos, el número de parejas es 5. Si quisieramos sumar 200 términos, el numero de parejas sería 100 y, en general, si queremos sumar n términos, el número de parejas es n/2.
Por lo tanto, la suma de n términos de cualquier progresión aritmética será igual a la suma del primero con el último multiplicada por el número de parejas, lo que nos da la siguiente fórmula:
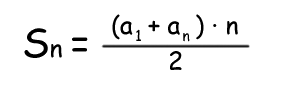



 RSS: Entradas
RSS: Entradas
267 Responses to Progresiones Aritméticas