Cuando el año pasado medimos en el Instituto el radio de la Tierra, le comenté a un amigo que lo habían hecho los griegos, pero que después volvimos a pensar que la Tierra era plana hasta los tiempos de Colón. ¡Más de 1500 años con un conocimiento perdido! Un tiempo después, en una conversación telefónica, mi amigo me dijo que se lo había contado a su novia y que ésta le había contestado: “¿Pero los griegos no hablaban con los hijos, o qué?”.
 Lo cierto es que ese tema (la pérdida de conocimientos) siempre me ha preocupado. De hecho, una de las bases sobre las que inicié este blog, tal día como hoy hace ya tres años, fue el relato de Isaac Asimov “La Sensación De Poder”, en el que se cuenta cómo un simple técnico redescubre los algoritmos para multiplicar y dividir utilizando sólo lápiz y papel. Pues bien, hace unos días con el periódico “El Norte de Castilla” comenzó una promoción de “Juegos de Ingenio”. El primer juego de la colección era el poliedro estrellado, que consiste en seis piezas de madera encajadas de tal forma que parece imposible volverlo a montar en caso de que se desarme. Precisamente por eso está catalogado como Juego de Ingenio, porque hay una manera, ingeniosa, de montarlo.
Lo cierto es que ese tema (la pérdida de conocimientos) siempre me ha preocupado. De hecho, una de las bases sobre las que inicié este blog, tal día como hoy hace ya tres años, fue el relato de Isaac Asimov “La Sensación De Poder”, en el que se cuenta cómo un simple técnico redescubre los algoritmos para multiplicar y dividir utilizando sólo lápiz y papel. Pues bien, hace unos días con el periódico “El Norte de Castilla” comenzó una promoción de “Juegos de Ingenio”. El primer juego de la colección era el poliedro estrellado, que consiste en seis piezas de madera encajadas de tal forma que parece imposible volverlo a montar en caso de que se desarme. Precisamente por eso está catalogado como Juego de Ingenio, porque hay una manera, ingeniosa, de montarlo.
La sorpresa me la llevé cuando abrí el papelito con la supuesta solución y me encontré con esto:
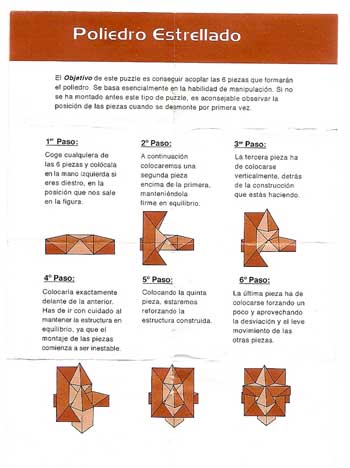
La última pieza hay que colocarla “forzando un poco y aprovechando la desviación y el leve movimiento de las otras piezas”. ¿Forzando un poco? ¿Aprovechando la desviación y el leve movimiento? ¿Pero de qué van? ¿Quién escribió esas instrucciones? Precisamente esa es la forma en que uno intentaría hacerlo pero, si las piezas están bien hechas, no se puede. La forma de montarlo es haciendo dos estructuras de tres piezas cada una, de manera que estas dos piezas encajan perfectamente una en la otra, sin forzar nada, sin aprovechar ningún movimiento.
Me pregunto cuánta gente que no conociera el juego y que lea estas instrucciones se las crea, y se las diga a los amigos con los que comparta el puzzle. Si no hubiera nadie que transmitiera la forma correcta de hacerlo, en unos años todo el mundo pensaría que esta es la “forma” correcta de hacerlo. Me imagino que es así como funciona la pérdida de conocimientos. Los que enseñan la manera errónea acaban siendo mayoría y llega un día en que nadie recuerda la forma correcta. Como hacer una raíz cuadrada. Creo que sólo saben hacerla a mano el 90% de los profesores de matemáticas y de los alumnos de 1º de ESO. A partir de 2º, la forma correcta de hacerla es utilizando la calculadora. En unos años, los profesores de matemáticas no sabrán hacerla y dejarán de enseñarla. Los nuevos libros no recogerán el algoritmo y los viejos libros de texto ya sabemos que no los abrirá nadie porque habrán caducado.
Y quizá sea mejor así. La calculadora las hace más rápido y saca más decimales. Si dejan de enseñarse, en 1º de ESO habría más tiempo para enseñar otras cosas más útiles que un algoritmo que seguramente no use el 99% de la población mundial. Habría que darle las gracias al inventor del mismo y decirle que su tiempo ya pasó, que las máquinas han superado su método, igual que éste superó a los antiguos métodos egipcios y babilónicos. C’est la vie.
Pero cuando el conocimiento que se pierde es que la Tierra es redonda…



 (4,00 / 5. Hay
4 votos)
(4,00 / 5. Hay
4 votos)


 RSS: Entradas
RSS: Entradas
4 Responses to Pérdida de conocimientos