Herramienta para obtener números aleatorios de 5 cifras sin repetición (las cinco cifras son diferentes). Automáticamente sale uno. Si quieres obtener más, pulsa “Obtener otro”.
Explicación:
Se trata de contruir números de 5 cifras con las 10 cifras disponibles (de 0 a 9) sin repetirlas, es decir, una vez que hemos puesto el 4, ya no podemos usarlo. Así, el número 36821 es posible, pero no lo es el 25759, ya que la cifra 5 se repite.
A esto se llaman variaciones sin repetición. El número de variaciones sin repetición que podemos formar es fácil de obtener. Veámoslo con un ejemplo:
Disponemos de 10 elementos (las cifras del 0 al 9) y queremos hacer grupos de 5 sin repetir elementos. Para la primera cifra, tenemos 10 posibilidades. Una vez elegida una, para la segunda cifra solo nos quedan 9 opciones (las cifras del 0 al 9 sin contar la que ya hemos cogido). Para la tercera cifra habra 8 posibilidades, 7 para la cuarta y 6 para la quinta y última.
En total, tenemos 10*9*8*7*6 formas distintas. Es decir, podemos escribir 10*9*8*7*6 números distintos en los que no se repite ninguna cifra.
En el caso general, el número de variaciones sin repetición de n elementos tomados de m en m, es:
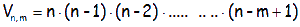
O lo que es lo mismo:
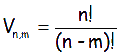
Si se pudiesen repetir cifras, sería mucho más sencillo, ya que en cada posición tendríamos 10 opciones, por lo que en total tendríamos 10·10·10·10·10, es decir, 105. En el ejemplo anterior, es fácil ver que el número de variaciones con repetición de 10 elementos tomados de 5 en 5 es 10.000, es decir, que podemos escribir 10.000 números distintos de 5 cifras (es evidente, desde el 00000 hasta el 99999).
La fórmula general para este caso es:
VRn,m = nm



 RSS: Entradas
RSS: Entradas