Herramienta para calcular operaciones con números complejos. Escribe en las casillas los números complejos que tengas y pulsa el boton de la operación que quieras realizar.

Explicación:

Los números complejos surgen para dar solución a ecuaciones del tipo x²+1=0, es decir, aquellas en las que aparecen raíces cuadradas de números negativos.
Como sabemos, la raíz cuadrada de un número negativo no tiene solución en los números reales, ya que cualquier número real elevado al cuadrado da un resultado positivo.
Ahí es donde aparece el número i, la unidad de los números imaginarios. El número i no es ni más ni menos que 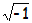, de modo que:

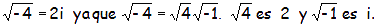
Estos son los llamados números imaginarios. Si queremos sumar un número real (a) con un número imaginario (bi), nos queda:

a + bi

que es lo que se llama número complejo.

Los números complejos, por tanto, están formados por una parte real y una parte imaginaria. La forma de operar con ellos es similar a la que se utiliza con los binomios a + bx. Así:

SUMA:

Se suman por separado las partes reales y las imaginarias.

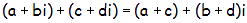
RESTA:

Se restan por separado las partes real y las imaginarias.

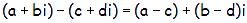
PRODUCTO:

Se multiplican todos los términos entre sí, y se simplifica el resultado, teniendo en cuenta que i·i=-1.

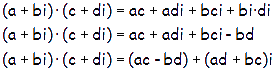
DIVISIÓN:

Se multiplican, tanto el numerador como el denominador, por el conjugado del denominador:

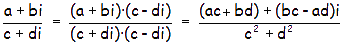
Observa que (c + di)·(c – di) = suma por diferencia = diferencia de cuadrados = c² – (di)² = c² – d²i² = c² + d²