Sigue el ritmo

Leo, vía “El País”, un artículo del periódico de México “El Universal” que dice:

Me llama la atención la frase: “A ese ritmo, en dos años estaríamos en mil ejecuciones al mes” y me pregunto: ¿A qué ritmo exactamente?
Imagino que, olvidándose del día del mes, hace la serie Septiembre, Julio, Mayo que, si la continuamos, nos daría Marzo, Enero. Es decir, en dos años se alcanzarían las mil muertes en Enero, como indica el autor.

Ahora bien, si no nos fijamos solamente en el mes, sino también en el día, ya que disponemos de los datos, tenemos que el 12 de Septiembre es el día 255 del año, el 1 de Julio es el día 182 y el 15 de Mayo, como se indica en el artículo, el 135.
Si representamos en una gráfica los días que se tarda en llegar a las mil muertes frente al año, tenemos lo siguiente:

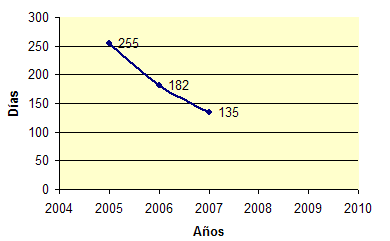
El autor del artículo ha supuesto que esos datos se ajustan a una recta, y la ha continuado, obteniendo lo siguiente:

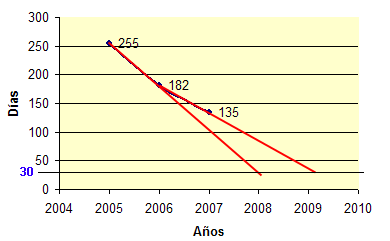
Dado que ninguna recta pasa por los tres puntos a la vez, cualquier recta aproximada que pase cerca de los tres puntos alcanzará el valor y=30 en un punto intermedio entre los dos dibujados (2008 y 2009, aproximadamente), con lo que se cumple lo dicho por el autor: en 2009 se alcanzarían los 1000 muertos en el mes de enero.Pero, disponiendo de tres puntos y viendo su representación, uno diría que los datos se ajustan mejor a una parábola o a una exponencial decreciente. Si buscamos la parábola (o función cuadrática) que pasa por los tres puntos, obtenemos la función:

donde x es el año y F(x) los días que tardan en alcanzarse los mil muertos. Podéis (deberíais) comprobar que se cumple para 2005, 2006 y 2007 (los datos disponibles) y que, si la continuamos, obtenemos la siguiente grafica:

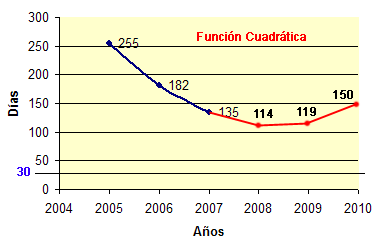
Vemos que, “a ese ritmo”, nunca se alcanzarían los mil muertos antes de Abril y, además, la situación mejoraría a partir de 2008.

Por último, si ajustamos los 3 datos disponibles a una exponencial, obtenemos la función:

Podéis (ejem) comprobar que esa función también cumple los datos conocidos y que, de continuarla, obtendríamos:

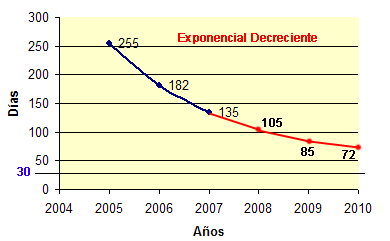
En este caso, nunca se alcanzaría el valor 30. De hecho, tiene una asíntota horizontal en y=49, es decir, “a ese ritmo” la situación se estabilizaría en alcanzar los mil muertos alrededor del 20 de Febrero (resultado igual de espeluznante que el predicho por el autor del artículo)

Por supuesto, los datos podrían igualmente ajustarse a funciones trigonométricas, polinómicas de mayor grado, etc. Matemáticamente, hay unas infinitas funciones que pasan por 3 puntos, con lo cual, hablar de “ritmo”, parece un poco precipitado. Es por ello que siempre se pide mucha más cautela al extrapolar datos (obtener puntos de fuera del intervalo conocido) que al interpolar (obtener puntos de dentro del intervalo conocido). Alguien les debería enseñar estas cosas a los periodistas…

Un problema parecido (el mismo, en realidad) es el que tienen los astrofísicos con la evolución futura del Universo que, para no hacer esto más largo, me apunto para una futura entrada.