Herramienta para calcular el número de variaciones de n elementos en grupos de k elementos. Introduce el número en la caja y pulsa “Calcular”. Para ver los agrupamientos, pulsa “Agrupamientos”.
Explicación:
Las variaciones de n elementos tomados en grupos de k son las diferentes formas de ordenar k elementos elegidos de un conjunto de n elementos. Por ejemplo, si tenemos 3 elementos, A, B y C, y queremos hacer grupos de dos elementos sin que se repitan, podemos hacerlo de 6 formas:
Esto es porque, en el primer lugar, podemos colocar cualquiera de los 3 elementos (A, B o C); como no se pueden repetir, en el segundo lugar podemos poner uno de los dos que no hemos puesto. Esto es, 3·2 = 6.
En general, para n elementos tomados de k en k, la fórmula es:
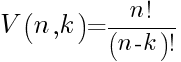
Si se pueden repetir, entonces tendríamos 9 formas de hacerlo:
Ya que en este caso, en primer lugar podemos poner cualquiera de los 3 elementos y, en el segundo, también cualquiera de los 3 elementos, es decir, 3·3 = 9.
En general, para n elementos tomados de k en k, con repetición, la fórmula es:
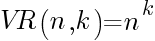



 RSS: Entradas
RSS: Entradas