Herramienta para calcular elementos desconocidos de una elipse. Introduce los datos que conozcas (con dos es suficiente), deja en blanco los desconocidos y pulsa “Calcular”.

Explicación:

Una elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos dados, F y F’, llamados focos, es constante.
Es decir, fijados dos puntos F y F’, uniendo todos los puntos P del plano que cumplan que PF + PF’ = constante, obtenemos una elipse. En el siguiente dibujo, PF + PF’ = QF + QF’ = RF + RF’, luego P, Q y R son puntos de la misma elipse, junto con todos los demás puntos que cumplan esa propiedad. (Pon el ratón sobre el dibujo para ver la elipse):

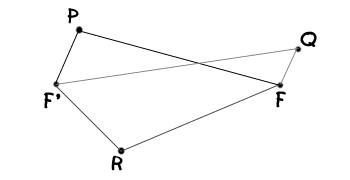
El “diámetro” más largo se llama eje mayor, que mide 2a, y el “diámetro” más corto se llama eje menor y mide 2b. Los focos siempre están en el eje mayor y la distancia entre ellos es de 2c,
llamada distancia focal.

En el siguiente dibujo,

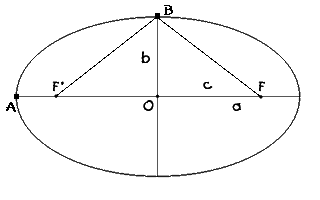
si nos fijamos en el punto A, vemos que AF + AF’ = 2a. Como el punto B también pertenece a la elipse, necesariamente se tiene que cumplir que BF + BF’ = 2a, por lo que la distancia desde B hasta F, que es la hipotenusa del triángulo rectángulo de catetos b y c, vale a. Por el teorema de Pitágoras, tenemos que:

a² = b² + c²

relación que se cumple en todas las elipses.

Por otra parte se define la excentricidad e como el cociente c/a, y nos da una medida del “achatamiento” de la elipse. La excentricidad puede tomar valores entre 0 y 1: Si vale 0, significa que c=0, es decir, los focos coinciden, por lo que tenemos una circunferencia (achatamiento nulo), y si vale 1, significa que c=a, es decir, tenemos una recta (achatamiento máximo).