Herramienta para calcular varios elementos de una parábola. Introduce los datos de la función y pulsa “Resolver”.

Explicación:

Una función cuadrática es aquella de la forma y = ax² + bx + c. Si la representamos gráficamente, obtenemos una parábola. Vamos a ver cómo se calculan los elementos de esa parábola:

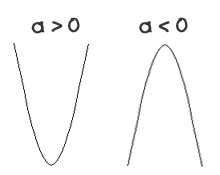
ORIENTACIÓN: Para saber si una parábola está abierta hacia arriba o hacia abajo, tan solo hay que mirar el término ax². Si a es positivo, está abierta hacia arriba, y si es negativo, hacia abajo.

VÉRTICE: Es importante calcularlo, ya que es el máximo o el mínimo de la parábola, dependiendo de su orientación. Si queremos dibujarla, es un punto clave. Calcularlo es sencillo, ya que la coordenada x es -b/2a. Para hallar la coordenada y, basta con sustituir en la fórmula el valor de la x. Por ejemplo, en la parábola y = x² – 4x + 5, el vértice estará en:

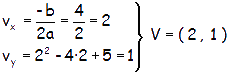
EJE DE SIMETRÍA: El eje de simetría siempre es vertical, y pasa por el vértice, luego su ecuación será:

x = v_x es decir, x = -b/2a

En el ejemplo anterior, el eje de simetría tiene por ecuación: x = 2

PUNTOS DE CORTE CON LOS EJES: En el eje Y la coordenada x es cero, luego, sustituyendo este valor en la fórmula, hallamos la y:

y = a·0² + b·0 + c = c, por lo que el punto de corte es el ( 0 , c )

En el eje X, es la y la que vale cero. Sustituimos en la fórmula y hallamos los valores de x:

0 = ax² + bx + c

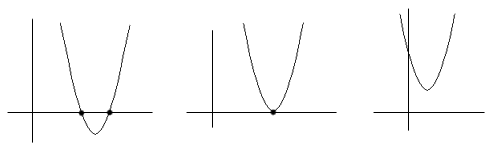
Tenemos una ecuación de segundo grado, que puede tener dos soluciones, una o ninguna, es decir, la parábola puede cortar al eje X en dos puntos, en uno o en ninguno: