Uno puede estimar, casi sin dificultad, que del punto en el que está a otro que se ve a lo lejos hay 10 metros, 50, 100 o 200. Distancias mayores en campo abierto nos resultan un poco más complicadas y podemos decir que hay 5 Kilómetros donde sólo hay 2 o viceversa. Si pasamos a superficies, ya muy pocos se defienden sin pasar antes por la estimación de distancias. Por ejemplo, si os pregunto cuántos metros cuadrados tiene la pared de vuestra habitación, muchos tendréis que hacer el cálculo (más o menos 3 de largo, por algo más de 2 y medio de alto… unos 8 m2 aproximadamente). Estimar 200 m2 o 1500 m2 está al alcance de muy pocos. Los de la tele pasan directamente a la siguiente unidad de superficie: el campo de fútbol, y construyen frases tan precisas (en lo matemático y el lo lingüístico) como: “Eso era como 7 campos de fútbol”. La pregunta es: “¿Cuántos metros cuadrados tiene un campo de fútbol?” ¿Alguién sabe responder a esa pregunta en un tiempo relativamente corto?
Bien, pues si las superficies ya nos plantean tantas dificultades, imaginad el volumen. A ver, alguien que, mientras lea esto, se haga una imagen mental de unos 100 m3, o de 1 hectómetro cúbico (¿Son lo mismo?) Fijáos en el chiste de Forges publicado hace tiempo en “El País”:

“El País”, Lunes 8 de Agosto de 2005
Si el cubo es un Hectómetro cúbico, significa que mide un hectómetro de largo, otro de ancho y otro de alto, es decir, 100 metros por 100 metros por 100 metros. Si esto es así, el tipo de la viñeta, que aproximadamente mide la cuarta parte, mediría unos 25 metros de altura… lo cual me parece mucho para una persona.
Suponiendo que la persona de la viñeta midiera 2,5 metros (que ya es decir), en vez de los 25, el cubo sería un Decámetro cúbico, es decir, que el hectómetro cúbico serían nada menos que ¡1000 cubos! como el del dibujo. Casi nada. Ya véis, “un hectómetro cúbico” se dice rápido, pero es más grande de lo que pensábamos.
Ahora os voy a proponer un ejercicio mental: Imaginad que cogéis el carro de un supermercado (de los que dan calambre y siempre se desvían hacia un lado), y váis echando los productos de la siguiente lista. Tenéis que ir haciendo una estimación del volumen que ocupan, por si necesitaráis otro carrito. Aquí está la lista:
Un pack de 6 zumos de 200 ml.
Un zumo de 1 L.
Una botella de refresco de cola de 2 litros.
Una botella de agua de 1’5 L.
4 latas de 33 cl.
Una botella de 150 ml.
Una botella de cristal de 27’5 cl.
Otra lata de 33 cl.
Una bolsa de patatas fritas, de las de 170 gr. (las grandes)
Un bote de aceitunas de 150 gr.
Una bolsa de gominolas de 150 gr.
Una caja de Caldo para paellas.
Una caja de 4 barritas energéticas de 24 gr.
Otra barrita energética suelta.
Cuatro sobres de sopa de 125 gr.
Una bolsa de 45 gr. de cacahuetes con chocolate.
Una bolsa de alitas de pollo de 190 gr.
Una bolsa de snacks de 60 gr.
Una caja de 20 sobres de manzanilla.
Un bote de café molido de 100 gr.
Y un bote de mayonesa de 450 ml.
¿Qué tal ha ido? ¿Os ha llegado con un carro? ¿Os ha sobrado mucho? ¿Poco? ¿Habéis necesitado otro carro? ¿Otros dos? Pues esa es la lista de los productos que regala Marca en su nueva promoción y ésta es la foto del carro que les ha salido a ellos (o a sus publicistas):  (Pica en ella para verla grande). Más o menos lo mismo que habíais pensado, ¿verdad?
(Pica en ella para verla grande). Más o menos lo mismo que habíais pensado, ¿verdad?
Pues bien, todo ello es, por supuesto, completamente gratisasterico. Vale, tienes que juntar 15 cupones (15 periódicos) y pagar 6’95 € por gastos de distribución, pero sigue siendo gratis* (gratisasterisco, como dije) y, lo mejor de todo, NO ES publicidad engañosa, ya que hay leyes sobre ese tema y está prohibida (Ley 34/1988, de 11 de noviembre, General de Publicidad. Título II. Artículos 3b, 4 y 5).
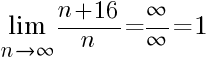
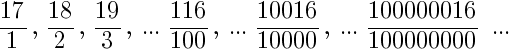



 (4,20 / 5. Hay
10 votos)
(4,20 / 5. Hay
10 votos)

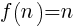 y seguramente nos lo den por bueno. Si decimos que es el 14, nos dirán que es incorrecto. Sin embargo, 14 es el número que continúa esa serie si seguimos la siguiente fórmula:
y seguramente nos lo den por bueno. Si decimos que es el 14, nos dirán que es incorrecto. Sin embargo, 14 es el número que continúa esa serie si seguimos la siguiente fórmula: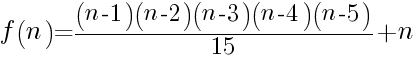
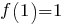 ,
, 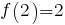 ,…
,… 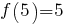 y
y 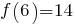 . Por lo tanto, no se trata de encontrar “una” pauta, sino “la” pauta, que es la que el examinador (o quien sea) quiere que digamos. Es por esto que estos ejercicios no gustan a muchos profesores, porque da la impresión de que en vez de fomentar que el alumno piense por sí mismo, se fomenta que piense como nosotros queremos que piense. Para estos casos la mejor recomendación es hacer uso de la Navaja de Occam, que viene a decir que:
. Por lo tanto, no se trata de encontrar “una” pauta, sino “la” pauta, que es la que el examinador (o quien sea) quiere que digamos. Es por esto que estos ejercicios no gustan a muchos profesores, porque da la impresión de que en vez de fomentar que el alumno piense por sí mismo, se fomenta que piense como nosotros queremos que piense. Para estos casos la mejor recomendación es hacer uso de la Navaja de Occam, que viene a decir que: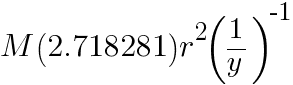










 RSS: Entradas
RSS: Entradas