Herramienta para calcular potencias de un binomio, tanto de una suma como de una resta. Introduce el exponente en la caja y pulsa “Calcular”.

Explicación:

El cuadrado de una suma (a + b)² o el cuadrado de una resta (a – b)² son sólo los casos más sencillos cuando elevamos un binomio a una potencia. Para estos casos, son conocidas las fórmulas “el cuadrado del primero más (o menos) el doble del primero por el segundo más el cuadrado del segundo”, es decir:

Si generalizamos esto para cualquier exponente n, tenemos lo que se conoce como “Binomio de Newton”. Según esta fórmula, los coeficientes del desarrollo de (a + b)ⁿ son los números combinatorios 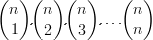de forma que en cada término, el grado de a va disminuyendo de uno en uno y el de b aumentando de uno en uno (así la suma de los exponentes siempre es n), con lo que obtenemos:

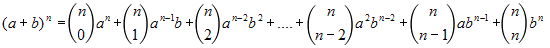
Precisamente esos coeficientes son los números de la fila enésima del Triángulo de Tartaglia:

Por ejemplo, si elevamos a la sexta potencia, los coeficientes son los números del triángulo de Tartaglia de la fila del 6, es decir, 1, 6, 15, 20, 15, 6 y 1, con lo que obtendríamos:

Si lo que elevamos es una resta, es igual pero alternando los signos más y menos, es decir: